Global impacts of heat and water stress on food production and severe food insecurity

The GTAP-DynW mannequin is a big dimensional CGE mannequin that makes use of the in depth GTAP (International Commerce Evaluation Undertaking) Knowledge Base Model 10⁵⁷ during which international locations or areas work together, importing items and companies from one another. GTAP-DynW is a (forward-looking) intertemporal slightly than a recursive CGE mannequin and consists of 18 Agro-Financial Zones⁵⁸ to characterize local weather, soil, and terrain circumstances pertinent to agricultural manufacturing⁵⁹. Following Kompas and Van Ha¹⁶ and Kompas et al.¹⁵, the mannequin additionally consists of local weather change harm features.

In GTAP-DynW, inside every nation or area, a producer combines inputs (land, labor, capital, an intermediate good, and pure sources) to supply a single good or service, which is consumed domestically by regional households (i.e., remaining consumption) and producers (i.e., intermediate demand for merchandise as inputs within the manufacturing of different commodities) or is exported to different worldwide or regional households and producers. Producers account for future impacts and coverage settings as per the next system of movement equations:

the place ({p}_{r,t}^{Okay}) and ok_r,t are the rental worth of capital and the capital inventory in area r at time t; ({p}_{r,t}^{I}) is worth of an funding good; δ_r is the capital depreciation charge; ψ_r is the capital increment from the (gross) funding exercise; i_t is the worldwide rate of interest; ({phi }_{r}) is an funding increment coefficient; and µ_r,t is the shadow worth of capital.

Water stress results

The manufacturing of agriculture output (Q_j,t) is approximated by a continuing elasticity substitution (CES) manufacturing operate that features the demand for commodity i to be used by j (QF_i,j,t) from each home and imported sources, and the worth added within the business j (QVA_j,t). The demand of endowments (QSE_i,j,t) that features the 18 AEZ land use classes and pure sources for the worth added within the business j (QVA_j,t) is given by:

the place afe_i,j,t is augmenting technological change of the endowments i by j; PSE_i,j,t is the market worth of ‘sluggish’ endowment i (e.g., land which is tough to reallocate) utilized by business j; PV A_j,t is the agency’s worth of worth added in business j; and γ_j,t is the elasticity of transformation for sluggish major issue endowments within the manufacturing of value-added in j.

Beneath the impact of water and warmth stress, with local weather change, the effectiveness of land use for agriculture or AEZ land decreases, the place the relative discount within the effectivity of land endowments is immediately proportional to the relative improve in water stress. In GTAP-DynW, water stresses are derived from WRI⁶⁰. This world GIS water knowledge of 15,006 basins was spatially merged with the worldwide GIS layers Esri-USGS⁶¹ to generate a geographical water stress projection for 174 international locations, after which mapped to accord with GTAP-DynW’s 30 combination international locations/areas. Water stress at a time by a area i is estimated from the projection of water stress in all basins j positioned within the area i with a weighted coefficient of j that’s measured as the world or share of j within the whole basin space in i, or

the place wsb(i, j) is the water stress of a basin j (within the set of J basins positioned in area i), i belongs to the GTAP-DynW’s 30 areas (I); and B(i, j) is the world of basin j positioned in i.

Water stress impacts land use by AEZ by area and time in QFE_i,j,t and adjustments QVA_j,t and, thus, agricultural manufacturing (Q_j,t). The water stress indicators are deviations (i.e., an excessive amount of and too little) from the 2020 baseline underneath the impact of local weather change, following WRI⁶⁰, and are quantified just for irrigated agriculture. The magnitudes of the water stress shock by AEZ is dependent upon the share of irrigated land in whole land use within the area’s AEZ (w_c,irr) and the change of irrigated water quantity in that AEZ in a area (dIW_c,t), is given by:

the place c, j, t represents 18 AEZ land sorts, agricultural commodity, and time.

To calibrate the influence of water stress on agricultural outputs, we assumed a continuing elasticity of substitution (CES) manufacturing operate and outlined calls for for intermediate inputs (QF_i,j,t) by:

the place Q_j,t is the agricultural output of commodity j; pf_i,j,t is the agency’s worth for enter commodity i to be used by j; ps_j,t is the availability worth of commodity j; A_i,j,t is the composite regional variable of augmenting know-how change; and γ_j,t is the elasticity of substitution amongst composite intermediate inputs within the agricultural sector j. Two particular augmenting know-how change variables embrace a water stress issue (afw1_i,t) for intermediate inputs and endowments used for manufacturing, and a region-specific common charge of intermediates augmenting know-how change of j (afw2_j,t).

The shock afw1_c,j,t is dependent upon the weighted coefficient of irrigated land in whole land use for an agricultural crop w_irr,j, the change of irrigated water by time (dIW_c,t), and the water stress coefficient to crop yields, or

the place c, j, t represents 18 AEZ land sorts, agricultural commodity, and time. Water costs from water sources paid by water person industries are added to regional earnings, but additionally improve prices in these sectors that will trigger a shift or reallocation of water use amongst water utilizing industries. For a water worth pwater(t) in a area r, the worth index for purchases of ok commodity by j sector in area r (PFE_j,ok,r,t) is given by:

the place VFA_j,ok,r,t is the acquisition and agency’s tax of ok inputs to be used by sector j; p_j,ok,r,t is the market worth of ok to j; taxF_j,ok,r,t is the tax on agency’s purchases of ok by manufacturing j; pwater_r,t is water worth at t; and WIN_j,ok,r,t is the water depth of j on ok. Thus, a water stress shock causes a change in PFE_j,ok,r,t and a shift in water withdrawals from home and imported sources is dependent upon the home and import commodity combine.

Warmth stress results

Harm features present the relationships between local weather variables (reminiscent of common temperature, humidity, or excessive warmth days) on productiveness, earnings, and useful resource endowments⁶². Roson and Sartori⁶² present the estimated parameters of harm features for 120 GTAP international locations and areas utilizing GTAP9 with six local weather impacts: sea degree rise, variation in crop yields, warmth stress results on labor productiveness, human well being, tourism, and family vitality demand. Projections from GTAP-DynW embrace harm features associated to warmth stress and their impacts on agricultural outputs and labor productiveness within the agricultural sector utilizing GTAP10a. The warmth stress shocks from world warming (e.g. losses in agricultural and labor productiveness) are primarily based on Kompas et al.¹⁵, Kompas and Van Ha¹⁶, and Roson and Sartori⁶².

Meals safety results

In GTAP-DynW, every meals commodity comprises dietary elements with totally different vitality consumption (energy). The aggregated dietary provide within the area r (S(r, t)) (measured as Giga-calories (GCal)) is aggregated as a sum of dietary provide from meals manufacturing i or

the place S(i, r, t) is meals manufacturing i (thousand tons); and z(i) is the diet conversion elements of meals i for calculating that meals’s vitality content material from one ton of meals i to energy. The common every day diet consumption a required for human meals safety is taken as given, and varies by nation and area (supply knowledge: FAO^22,63,64) and is given by:

the place a is common every day diet in energy. International meals manufacturing (GCal) is the sum of all regional meals provide and the overall inhabitants throughout areas is F(r,t).

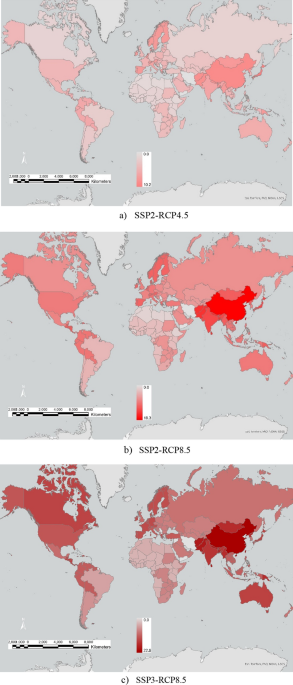
The variety of individuals with extreme meals insecurity, in thousands and thousands, is decided by the hole within the minimal calorie demand and the accessible manufacturing and is given by:

the place dS(r, t) is the discount of meals manufacturing in area r at t to the bottom dietary provide (S(r, 0)).

The meals insecurity charge (RIF(r, t)) is the ratio of the variety of individuals with extreme meals insecurity over the overall inhabitants of that nation or POP (r, t):

The worldwide discount of meals manufacturing (dS(t)) is the sum of the discount of meals provide (dS(r, t)) throughout all areas. The worldwide variety of individuals with extreme meals insecurity (IF (t)) is the sum of all areas’ individuals with extreme meals insecurity ensuing from the discount of meals provide (or IF (r, t)).